МЕТОДЫ ПОСТРОЕНИЯ МАГИЧЕСКИХ КВАДРАТОВ

 

Часть V

 

Раздел 2. Построение магических квадратов чётно-чётного порядка

 

Перехожу к описанию методов построения магических квадратов чётно-чётного порядка, то есть порядка кратного 4: n=4k, k=1, 2, 3…

Кратко некоторые методы изложены в статье

 

http://www.klassikpoez.narod.ru/metody.htm

 

 

МЕТОД КВАДРАТНЫХ РАМОК

 

Как я уже упоминала, метод квадратных рамок был найден мной очень давно в журнале “Наука и жизнь”. Сейчас встретила этот метод в книге Ю. В. Чебракова. Автор называет этот метод методом террас.

 

Рассмотрим построение данным методом магического квадрата восьмого порядка. На матричное поле (с изображённым на нём исходным квадратом 8х8) наносятся квадратные рамки со стороной в два раза меньшего размера, чем сторона исходного квадрата (см. рис. 1) с шагом в одну клетку по диагонали (или две клетки по строкам и столбцам). Затем по линиям рамок расставляются числа от 1 до n² по порядку, начиная с левой верхней ячейки исходного квадрата, причём первая рамка обходится по часовой стрелке, вторая рамка начинается с верхней свободной справа ячейки квадрата и обходится против часовой стрелки и т. д. Числа, не попавшие в квадрат, переносятся внутрь его так, чтобы они примкнули к противолежащим сторонам квадрата. Готовый магический квадрат изображён на рис. 2.

 

			4	5
		3			6
	2		21	20		7
1		22			19		8
16	23		36	37		18	9
24	15	35			38	10	17
25	34	14	53	52	11	39	32
33	26	54	13	12	51	31	40
48	55	27			30	50	41
56	47		28	29		42	49
57		46			43		64
	58		45	44		63
		59			62
			60	61

 

                      Рис. 1

 

Примечание: здесь рамки не получились квадратными да ещё и немного сместились из-за неудобной графики компьютера.

 

 

 

                                                                       Рис. 2

 

Магические квадраты, построенные методом квадратных рамок, ассоциативны.

 

Приведу иллюстрацию из моей старой рукописи “Компьютер решает головоломки”. Рукопись была напечатана в 1993 г. на старой ЭВМ, но которой я работала. На иллюстрации показано построение магического квадрата 12-ого порядка методом квадратных рамок. Ячейки раскрашены цветным карандашом (печать на ЭВМ была, конечно, чёрно-белая). Надпись на иллюстрации сделана сейчас.

 

 

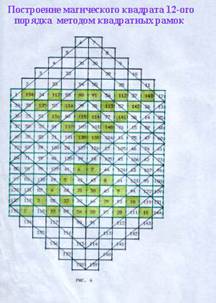
Понятно, что методом квадратных рамок можно построить только один магический квадрат данного порядка. Можно ли обобщить метод? Попробуем сделать это с помощью использования обратимых квадратов. Начнём с магического квадрата 4-ого порядка. На рис. 3 вы видите квадрат, построенный методом квадратных рамок.

 

 

                                                                       Рис. 3

 

Чтобы получить такой магический квадрат, применим к самому простому обратимому квадрату, матрицу которого обозначим A(a_ij), следующее матричное преобразование (рис. 4):

 

 

                                                                       Рис. 4

 

А теперь возьмём другой обратимый квадрат 4-ого порядка (рис. 5) и применим к нему это же преобразование.

 

 

                                                                       Рис. 5

 

На рисунке 6 вы видите готовый магический квадрат.

 

 

                                                                       Рис. 6

 

Мы получили новый магический квадрат, не эквивалентный квадрату на рис. 3. Эти два квадрат связаны преобразованием “плюс-минус 2”. Предлагаю читателям составить матрицу этого преобразования.

 

В статье http://www.geocities.com/~harveyh/most-perfect.htm приведено точное количество обратимых квадратов 4-ого порядка; их всего 48, три группы по 16 квадратов в каждой. Вот первая группа обратимых квадратов из этой статьи.

 

 

Первый квадрат – это самый простой обратимый квадрат, в нём числа записаны в естественном порядке.

 

Приведу ещё один пример применения матричного преобразования с рис. 4 к одному из обратимых квадратов. Возьму в качестве исходного последний обратимый квадрат (из приведённой выше группы обратимых квадратов). На рис. 7 вы видите построенный магический квадрат.

 

 

                                                                       Рис. 7

 

Этот квадрат получается из квадрата, построенного методом квадратных рамок (рис. 3), перестановкой строк и столбцов.

 

Таким образом, мы можем построить с помощью данного матричного преобразования 48 магических квадратов 4-ого порядка. Вот такое интересное обобщение метода квадратных рамок даёт использование обратимых квадратов.

 

Проделаем то же самое для квадратов 8-ого порядка. На рис. 8 вы видите матричное преобразование, которое надо применить к самому простому обратимому квадрату 8-ого порядка, чтобы получить магический квадрат, построенный методом квадратных рамок (рис. 2).

 

 

                                                                       Рис. 8

 

Берём теперь в качестве исходного квадрата другой обратимый квадрат, изображённый на рис. 9.

 

 

                                                                       Рис. 9

 

Применив матричное преобразование с рис. 8 к этому обратимому квадрату, получаем следующий магический квадрат (рис. 10):

 

 

                                                                       Рис. 10

 

Очевидно, что магические квадраты, построенные с помощью матричного преобразования, тоже ассоциативны (см. квадраты на рис. 6, 7, 10).

 

Новый магический квадрат 8-ого порядка связан с квадратом, построенным методом квадратных рамок, преобразованием “плюс-минус 4”. Вы видите матрицу этого преобразования на рис. 10а.

 

 

                                                                       Рис. 10а

 

Симпатичное преобразование, сохраняющее ассоциативность квадрата.

 

В указанной выше статье приведено количество обратимых квадратов 8-ого порядка, это 10 групп по 36864 квадрата в каждой, итого 368640 квадратов. Столько же магических квадратов мы можем построить с помощью показанного здесь матричного преобразования.

 

Понятно, что применение матричного преобразования легко запрограммировать. Если составить программу построения всех обратимых квадратов 8-ого порядка, то, добавив в эту программу блок применения к каждому обратимому квадрату матричного преобразования, вы построите с помощью этой программы 368640 магических квадратов 8-ого порядка. Все эти квадраты будут различны с точностью до перестановки строк и столбцов и преобразований типа “плюс-минус …”.

 

В статье http://www.klassikpoez.narod.ru/soversh3.htm я построила все 10 уникальных (то есть принципиально различных) обратимых квадратов 8-ого порядка. Каждый из уникальных обратимых квадратов порождает группу из 36864 обратимых квадратов. Построение всех обратимых квадратов – задача очень интересная ещё и потому, что из каждого обратимого квадрата другим матричным преобразованием (оно разработано мной при исследовании совершенных квадратов) можно получить совершенный магический квадрат.

 

На рис. 11 покажу третий уникальный обратимый квадрат 8-ого порядка (два уже представлены здесь, первый – самый простой обратимый квадрат, в котором числа записаны по порядку, второй – на рис. 9).

 

 

Рис. 11

 

Применим матричное преобразование с рис. 8 к этому обратимому квадрату. Полученный в результате магический квадрат вы видите на рис. 12.

 

 

                                                                       Рис. 12

 

***

 

Посмотрим на метод квадратных рамок с точки зрения латинских квадратов. Для этого разложим магический квадрат, построенный этим методом (рис. 2) на два ортогональных латинских квадрата. Смотрите эти квадраты на рис. 13 - 14.

 

 

                                                                       Рис. 13

 

Первый латинский квадрат получился обобщённый. Он, как и должно быть, является нетрадиционным ассоциативным магическим квадратом с магической константой 28. Очевидны некоторые закономерности в составлении этого латинского квадрата: 1)правая половина квадрата является зеркальным отражением левой половины; 2) в первом столбце числа записаны по порядку; 3) числа в нижней строке комплементарны числам в соответствующих ячейках верхней строки (то есть в сумме дают 7); 4) то же самое имеет место для чисел в любых двух симметричных строках.  Есть ещё некоторые, не такие очевидные, закономерности. Предлагаю читателям выявить эти закономерности. Достаточно ли этих закономерностей, чтобы составить латинский квадрат? Попробуйте ответить на этот вопрос. А для этого попытайтесь составить первый латинский квадрат для построения магического квадрата 12-ого порядка, разумеется, точно такого, какой строится методом квадратных рамок (этот квадрат вы видите на иллюстрации из книги “Компьютер решает головоломки”).

 

Вот второй латинский квадрат (рис. 14).

 

 

                                                                       Рис. 14

 

Второй латинский квадрат тоже обобщённый. Он так же является нетрадиционным ассоциативным магическим квадратом с магической константой 28. Как он составляется, трудно определить. Ясно одно: он должен быть ортогонален первому латинскому квадрату.

 

Интересно посмотреть на магический квадрат, который получится, если латинские квадраты поменять местами (рис. 15).

 

 

                                                                       Рис. 15

 

Получился новый магический квадрат с очень оригинальной начальной цепочкой. Продублирую здесь квадрат, построенный методом квадратных рамок, и выделю в нём начальную цепочку для сравнения (рис. 16).

 

 

                                                                       Рис. 16

 

Следовательно, применение латинских квадратов даёт нам как минимум ещё один новый магический квадрат.

 

Ну, и, конечно, в квадратах, построенных методом квадратных рамок, работают качели. Предлагаю любознательным читателям убедиться в этом самостоятельно.

 

***

 

Сейчас попробовала составить первый латинский квадрат для построения квадрата 12-ого порядка, который строится методом квадратных рамок. Для этого использовала те закономерности, которые выявлены в первом латинском квадрате 8-ого порядка (см. рис. 13). Первый латинский квадрат получился такой (рис. 17):

 

 

                                                                       Рис. 17

 

Все закономерности сохранены. Обратите внимание на то, как интересно в квадратах, построенных методом квадратных рамок, повторяется начальная цепочка. На рис. 17 раскрашены нулевой, первый и второй циклы качания качелей. Нулевой цикл, как знают читатели, соответствует числам начальной цепочки. Начальная цепочка повторяется попеременно то в таком же виде, то в перевёрнутом.

 

Итак, первый латинский квадрат для построения магических квадратов, строящихся методом квадратных рамок, мы составлять умеем. Осталось научиться составлять второй латинский квадрат (он должен быть ортогональным первому). Пока я не могу сказать, как это делается, и поэтому получаю второй латинский квадрат как дополнительный к первому по известному мне готовому квадрату, построенному методом квадратных рамок. Второй латинский квадрат изображён на рис. 18.

 

 

                                                                       Рис. 18

 

Оба латинских квадрата обобщённые и являются нетрадиционными ассоциативными магическими квадратами с магической константой 66.

 

Теперь осталось построить из полученной пары ортогональных латинских квадратов магический квадрат. Сначала построим магический квадрат, в точности совпадающий с квадратом, построенным методом квадратных рамок (рис. 19).

 

 

                                                                       Рис. 19

 

В магическом квадрате раскрашены наборы чисел, соответствующие нулевому, первому и второму циклам качания качелей (как и в первом латинском квадрате).

 

Теперь поменяем местами первый и второй латинские квадраты в формуле для построения магического квадрата (надеюсь, читатели помнят эту формулу). В результате мы получим новый магический квадрат 12 порядка с оригинальной начальной цепочкой. Смотрите этот квадрат на рис. 20.

 

 

                                                                       Рис. 20

 

В этом магическом квадрате “тон задаёт” латинский квадрат с рис. 18, потому что он в этом случае – первый. Продублирую этот латинский квадрат и сделаю соответствующую раскраску (рис. 21).

 

 

                                                                       Рис. 21

 

Незыблемый закон повторения начальной цепочки в циклах!

 

МЕТОД РАУЗ-БОЛЛА

 

Метод Рауз-Болла состоит в следующем: в данный квадрат чётно-чётного порядка вписываются числа в их естественном порядке, начиная с левой верхней ячейки. Затем в квадрате проводятся диагонали. Числа, расположенные во взаимно симметричных ячейках (относительно центра квадрата), через которые прошли диагонали, меняются местами, а числа, через которые диагонали не прошли, остаются на месте. Так, на рис. 22 диагонали пересекли восемь чисел, надо поменять местами взаимно симметричные: 1-16, 6-11, 13-4, 10-7. Готовый магический квадрат изображён на рис. 23. Можно поступить наоборот: оставить на месте числа, через которые прошли диагонали, а поменять местами числа, не попавшие на диагонали и симметрично расположенные относительно центра квадрата. На рис. 24 показан квадрат, построенный таким образом. Сравнив его с квадратом на рис. 23, вы видите, что это тот же квадрат, повёрнутый на 180 градусов вокруг центра квадрата.

 

 

1	2	3	4		16	2	3	13		1	15	14	4
5	6	7	8		5	11	10	8		12	6	7	9
9	10	11	12		9	7	6	12		8	10	11	5
13	14	15	16		4	14	15	1		13	3	2	16

 

Рис. 22                           Рис. 23                      Рис. 24

 

При построении методом Рауз-Болла магического квадрата восьмого порядка диагонали соединяют на только углы квадрата, но и середины его сторон, то есть диагонали проводятся в четырёх  угловых квадратах 4х4 (см. рис. 25); взаимно симметричных пар чисел, которые надо поменять местами, будет шестнадцать: 1-64, 10-55, 19-46, 28-37, 8-57, 15-50, 22-43, 29-36, 4-61, 5-60, 11-54, 14-51, 18-47, 23-42, 25-40, 32-33. На рис. 26 изображён готовый магический квадрат восьмого порядка, построенный методом Рауз-Болла.

 

 

1	2	3	4	5	6	7	8		64	2	3	61	60	6	7	57
9	10	11	12	13	14	15	16		9	55	54	12	13	51	50	16
17	18	19	20	21	22	23	24		17	47	46	20	21	43	42	24
25	26	27	28	29	30	31	32		40	26	27	37	36	30	31	33
33	34	35	36	37	38	39	40		32	34	35	29	28	38	39	25
41	42	43	44	45	46	47	48		41	23	22	44	45	19	18	48
49	50	51	52	53	54	55	56		49	15	14	52	53	11	10	56
57	58	59	60	61	62	63	64		8	58	59	5	4	62	63	1

 

   Рис. 25                                                                  Рис. 26

 

Примечание: описание метода приведено по журналу “Наука и жизнь” (к сожалению, номер журнала я не помню, так как это было очень давно, 70-е годы прошлого века).

Интересно отметить, что в книге Ю. В. Чебракова метод Рауз-Болла представлен как метод Деланэ – Мондезира. Чебраков описывает метод так: “Построим исходную таблицу размером n*n. Разделим исходную таблицу на квадратные блоки 4*4 и отметим в каждом блоке клетки, находящиеся на главных диагоналях. Для получения классического квадрата порядка n=4k остаётся во всех отмеченных клетках произвести замену находящихся в них чисел d_i на числа n*n + 1 - d_i” (стр. 116).

Исходной таблицей автор называет самый простой обратимый квадрат.

Очевидно, что метод, описанный Чебраковым, не что иное, как метод Рауз-Болла. Непонятно, почему у него он называется по-другому.

Следует добавить, что для получения классического квадрата можно наоборот числа в отмеченных ячейках оставить без изменения, а все остальные числа заменить на взаимно дополнительные (см. рис. 26а).

 

 

Рис. 26а

 

Очевидно, что магический квадрат, построенный методом Рауз-Болла, ассоциативен.

 

В журнале был приведён ещё упрощённый метод Рауз-Болла, но он мало интересен, так как приводит к эквивалентному магическому квадрату. Кратко упрощённый метод состоит в следующем: так же проводят в квадрате диагонали, а затем вписывают числа в естественном порядке, сначала заполняя ячейки, пересечённые диагоналями и пропуская ячейки, не пересечённые диагоналями, а потом наоборот, начиная теперь писать с нижней правой ячейки квадрата. На рис. 27 изображён квадрат 8-ого порядка, построенный упрощённым методом Рауз-Болла.

 

 

                                                                       Рис. 27

 

Как видите, этот квадрат эквивалентен квадрату с рис. 26 и в точности совпадает с квадратом на рис. 26а справа.

Покажу ещё один квадрат, построенный упрощённым методом Рауз-Болла (рис. 27а). В квадрате выделена начальная цепочка.

 

 

                                                                       Рис. 27а

 

Обратите внимание: в этом методе исходным квадратом является самый простой обратимый квадрат. Естественно, сразу возникает вопрос: можно ли применить метод к другому обратимому квадрату. Проверим. Возьмём в качестве исходного обратимый квадрат 4-ого порядка с рис. 5. Проделаем нужные перестановки чисел в этом квадрате. Готовый магический квадрат показан на рис. 28.

 

 

                                                                       Рис. 28

 

Получаем новый магический квадрат. Он связан с квадратом, построенным методом Рауз-Болла (рис. 23) преобразованием “плюс-минус 2”. Даже начальная цепочка изменила форму.

 

Аналогично тому, как это было сделано в методе квадратных рамок, можно составить матрицу преобразования, с помощью которого очень просто строить магические квадраты из обратимых. Предоставляю это читателям.

 

Таким образом, мы имеем обобщение метода Рауз-Болла: из каждого обратимого квадрата можно получить новый магический квадрат.

 

Посмотрим на метод Рауз-Болла с точки зрения латинских квадратов. Для этого разложим квадрат с рис. 26 на два латинских квадрата. Первый латинский квадрат вы видите на рис. 29.

 

 

                                                                       Рис. 29

 

Во-первых, разумеется, этот обобщённый латинский квадрат является нетрадиционным ассоциативным магическим квадратом с магической константой 28. Ещё четыре закономерности очевидны: 1) числа в противоположных ячейках симметричных строк комплементарны; 2) правая половина квадрата является зеркальным отражением левой половины; 3) числа в главных диагоналях записаны по порядку; 4) каждая строка составляется из двух комплементарных чисел. Менее очевидная закономерность: четвертинка квадрата, состоящая из третьего и четвёртого столбцов, является зеркальным отражением четвертинки квадрата, состоящей из первого и второго столбцов. Аналогично – для третьей и четвёртой четвертинок. Думаю, этих закономерностей вполне достаточно, чтобы составить первый латинский квадрат, например, 12-ого порядка. Попробуйте!

 

В первом латинском квадрате хорошо видно повторение начальной цепочки. Оригинальная начальная цепочка! Продублирую квадрат с рис. 26 и сделаю в нём соответствующую раскраску (рис. 29а).

 

 

                                                                       Рис. 29а

 

На рис. 30 вы видите второй латинский квадрат.

 

 

                                                                       Рис. 30

 

Очевидно, что второй латинский квадрат получается из первого поворотом на 90 градусов против часовой стрелки. Поэтому составление пары ортогональных латинских квадратов в случае метода Рауз-Болла легко запрограммировать.

 

Посмотрим на магический квадрат, построенный из пары этих ортогональных латинских квадратов, переставленных в формуле для построения магического квадрата (рис. 31).

 

 

                                                                       Рис. 31

 

Очевидно, что этот квадрат эквивалентен квадрату с рис. 26.

 

На рис. 32 представлен первый латинский квадрат для построения магического квадрата 12-ого порядка (такого, какой строится методом Рауз-Болла). Этот латинский квадрат составлен по выявленным выше закономерностям в первом латинском квадрате 8-ого порядка (рис. 29).

 

 

                                                                       Рис. 32

 

Повернув этот латинский квадрат на 90 градусов против часовой стрелки, мы получим второй латинский квадрат (рис. 33).

 

 

                                                                       Рис. 33

 

Не буду показывать квадрат, построенный из этой пары ортогональных латинских квадратов и в точности совпадающий с квадратом, построенным методом Рауз-Болла. Покажу квадрат, полученный из этой же пары латинских квадратов, но переставленных (рис. 34).

 

 

                                                                       Рис. 34

 

Как видите, магический квадрат получился эквивалентным квадрату, построенному упрощённым методом Рауз-Болла (см. рис. 27а), а также и квадрату, построенному методом Рауз-Болла. Такой результат получается потому, что латинские квадраты получаются друг из друга поворотом на 90 градусов, то есть с точки зрения нетрадиционных магических квадратов они тоже эквивалентны.

 

***

 

Другое обобщение метода Рауз-Болла даёт применение метода качелей. Этот вопрос рассмотрен в статье

 

http://www.klassikpoez.narod.ru/frenikl.htm

 

Поэтому не буду здесь дублировать эту тему.

 

В этой же статье подробно рассмотрен метод построения пандиагональных квадратов чётно-чётного порядка из ассоциативных квадратов – преобразование трёх квадратов.

 

***

 

МЕТОД ЛАТИНСКИХ КВАДРАТОВ

 

В книге Ю. В. Чебракова рассматривается метод построения магических квадратов чётно-чётного порядка с помощью двух обобщённых ортогональных латинских квадратов (стр. 119-120), как самостоятельный метод. Почему я говорю “как самостоятельный метод”? Потому что метод латинских квадратов применим к любому из представленных выше методов построения. При этом магические квадраты, построенные методом латинских квадратов, приведённым Чебраковым, получаются совершенными. Причём не просто пандиагональными (по терминологии Чебракова ”совершенный” = ”пандиагональный”), а именно совершенными в моей терминологии. Я называю совершенными такие пандиагональные магические квадраты, которые обладают несколькими дополнительными свойствами (по-английски такие квадраты называются “most perfect”).

Этот метод подробно изложен в статье

http://www.klassikpoez.narod.ru/latsov.htm

 

 

АЛГОРИТМ ФРЕНИКЛЯ

 

Удивительные магические квадраты порядка n=4k, k=1, 2, 4, 5… (k не равно 3m, m=1, 2, 3, 4…) строятся по алгоритму Френикля. Квадрат 8-ого порядка, построенный по данному алгоритму, был показан на форуме. Меня очень заинтересовал этот магический квадрат, и я посвятила алгоритму Френикля статью

 

http://www.klassikpoez.narod.ru/frenikl.htm

 

(в этой статье вы найдёте ссылку на форум, где был показан квадрат Френикля).

 

Я применила к квадрату Френикля метод качелей и построила несколько подобных квадратов. Подробности смотрите в указанной статье. Здесь я покажу только квадрат Френикля (рис. 35).

 

 

                                                                       Рис. 35

 

Оригинальнейшая форма начальной цепочки! И в квадрате работают качели.

 

Магические квадраты порядков кратных 12 по данному алгоритму не строятся. Известен полумагический квадрат Агриппа, построенный по этому алгоритму. Для квадратов 12-ого порядка я составила программу и с помощью программы убедилась, что не существует ни одного магического квадрата 12-ого порядка, имеющего начальную цепочку такой формы. Для квадратов других порядков кратных 12 это утверждение требуется доказать.

 

Квадраты 4-ого порядка, построенные по алгоритму Френикля, получаются не просто магическими, но и пандиагональными. Пример на рис. 36.

 

 

                                                   Рис. 36

 

Остаётся открытым вопрос: существуют ли пандиагональные квадраты других порядков, кроме 4-ого, построенные по алгоритму Френикля. Собственно задача, предложенная на форуме, и состояла в том, чтобы превратить квадрат Френикля 8-ого порядка в пандиагональный. Этот квадрат превращается в пандиагональной простой перестановкой столбцов, однако такая перестановка изменяет форму начальной цепочки. Видимо, Френикль безуспешно пытался построить пандиагональный квадрат с такой же начальной цепочкой, как в его магическом квадрате, но это у него не получилось. Не получилось это и у меня по программе, которую я составила для решения данной задачи.

 

***

 

МЕТОД ОКАЙМЛЁННЫХ КВАДРАТОВ

 

Этот метод аналогичен методу окаймлённых квадратов, изложенному в Разделе 1 для квадратов нечётного порядка. Но здесь есть одна особенность: в процессе окаймления мы получаем также квадраты порядка n=4k+2 (или чётно-нечётного порядка), а здесь рассматриваются квадраты чётно-чётного порядка. Тем не менее, метод очень интересен и его необходимо представить. Описание метода излагается по книге Ю. В. Чебракова.

Построение для порядков n=4k и n=4k+2 различно. Самый первый магический квадрат, который можно построить этим методом, имеет порядок n=6. Он строится окаймлением магического квадрата 4-ого порядка. Итак, сначала излагаются правила построения магического квадрата порядка n=4k+2.

 

1.      Построим любой магический квадрат порядка n-2.

2.      Увеличим все элементы этого магического квадрата на величину 2(n-1) и поместим полученный нетрадиционный магический квадрат в матрицу n*n так, чтобы с каждой стороны квадрата был свободный столбец (свободная строка).

3.      Заполним угловые ячейки матрицы n*n следующим образом: в левую верхнюю ячейку запишем число 3m - 1, в верхнюю правую – число 1, в нижнюю левую –  число d - 1, в нижнюю правую - число d - 3m + 1, где m = n/2, d = n² + 1.

4.      В оставшиеся свободными ячейки верхней строки поместим (произвольным образом) числа {2i + 1} и {d – 2j}, где i = 1, 2, …, m – 2, а j = 1, 2, …, m.

5.      В оставшиеся свободные клетки левого столбца поместим (произвольным образом) числа 2m – 1, {d – 4m – 1 – j}, {3m – 1 – i}, {3m – 1 + q, d – 2m – q}, где j = 1, 2, …, M + 1, i= 1, 2, …, M, q = 1, 2, …, M – 1, M = [m/2].

6.      Оставшиеся свободными ячейки нижней строки (правого столбца) заполним числами, комплементарными числам в противоположных ячейках верхней строки (левого столбца), то есть дающими в сумме (n² + 1).

 

Проиллюстрирую построение копией примера из книги. Автор выбрал для построения следующий магический квадрат 4-ого порядка (рис. 37):

 

 

                                                   Рис. 37

 

Результат выполнения пунктов 2-3 изображён на рис. 38.

 

 

                                                   Рис. 38

 

На рис. 39 вы видите результат выполнения пунктов 4-5.

 

 

                                                   Рис. 39

 

Примечание: при заполнении левого столбца у меня возникла загвоздка. По формуле d – 4m – 1 – j никак не могу получить числа 28 и 27, которые автор вписал в ячейки левого столбца. Имеем: d=37, m=3, j=1, 2. Какой должна быть формула, чтобы получить числа 28 и 27? Может быть, такой: d – 4m + 1 + j? Видимо, опечатка.

 

Выполнение последнего пункта совсем просто: записываем в противоположных ячейках комплементарные числа. Готовый магический квадрат 6-ого порядка вы видите на рис. 40.

 

 

                                                   Рис. 40

 

Поскольку числа в верхней строке и в левом столбце квадрата вписываются произвольно (кроме чисел в угловых ячейках), можно построить данным методом не один магический квадрат. Так, для квадрата 6-ого порядка будет 24 варианта заполнения верхней строки и 24 варианта заполнения левого столбца, а всего получается 576 вариантов заполнения. Следовательно, можно построить 576 магических квадратов 6-ого порядка. На рис. 41 изображён один из вариантов.

 

 

                                                   Рис. 41

 

Переходим к следующему порядку, n=8. Так как этот порядок относится к серии порядков n=4k, здесь правила будут другие. В качестве исходного по-прежнему берётся любой магический квадрат порядка n-2, то есть в данном примере 6-ого порядка. Автор берёт в качестве исходного только что построенный магический квадрат 6-ого порядка с рис. 41. Пункт 2 выполняется так же, как в описанных выше правилах. Результат выполнения этого пункта показан на рис. 42.

 

 

                                                   Рис. 42

 

Теперь опишу правила заполнения строк и столбцов в этой матрице. Начинаем с пункта 3 правил (точная цитата из книги).

“3. Для заполнения клеток верхней строки таблицы n*n используем числа {4i – 3, 4i, d – 4i + 2, d – 4i + 1}, где m = [n/2], M = [m/2], d = n*n + 1, i = 1, 2, …, M.

При этом, если m кратно четырём, то в крайнюю левую клетку верхней строки помещаем число m, а в крайнюю правую клетку – число 1. Если же m не кратно четырём, то в крайнюю левую клетку помещаем число m + 3, а в крайнюю правую клетку – число 4. Остальные из указанных выше чисел расставляем в свободных клетках верхней строки произвольным образом.

4. Пусть в верхней левой угловой клетке таблицы n*n находится число i, а в верхней правой угловой клетке – число j, тогда в нижнюю левую клетку таблицы помещаем число d – j, а в нижнюю правую клетку - число d – i.

5. В оставшиеся свободными клетки левого столбца таблицы n*n помещаем (произвольным образом) числа {2m + 2i – 1, d – 2m – 2i}, где i = 1, 2, …, m-1.

6. Оставшиеся свободными клетки нижней строки и правого столбца заполняем так, чтобы расположенные друг против друга числа были взаимно дополнительными”.

 

Взаимно дополнительными автор называет комплементарные числа. Заполняем по приведённым правилам матрицу с рис. 42. На рис. 43 изображён готовый магический квадрат 8-ого порядка.

 

 

                                                   Рис. 43

 

Для квадрата 8-ого порядка имеется 720 вариантов заполнения верхней строки и столько же вариантов заполнения левого столбца. Следовательно, методом окаймлённых квадратов можно построить 518400 магических квадратов 8-ого порядка. Это только для одного исходного квадрата 6-ого порядка.

 

На этом автор книги заканчивает свой пример. Мы пойдём дальше. Выполним следующее окаймление, то есть построим магический квадрат 10-ого порядка. Так как этот порядок принадлежит к серии порядков n=4k+2, соответственно надо пользоваться правилами для таких порядков. В качестве исходного магического квадрата 8-ого порядка возьмём только что построенный квадрат с рис. 43 (хотя, разумеется, можно взять любой другой магический квадрат 8-ого порядка). На рис. 44 вы видите результат выполнения пунктов 1-2.

 

 

                                                   Рис. 44

 

 Заполним свободные ячейки в этой матрице, выполнив пункты 3-6 правил. Готовый магический квадрат 10-ого порядка представлен на рис. 45.

 

 

                                                   Рис. 45

 

Точно так же, как в случае окаймлённых квадратов нечётного порядка, здесь получаются концентрические магические квадраты. Посмотрите, какие магические константы имеют вписанные нетрадиционные магические квадраты: S₄ = 202, S₆ = 303, S₈ = 404. Все эти константы кратны числу d = n² + 1. Забавная закономерность! Впрочем, магическая константа квадрата 10-ого порядка S₁₀ = 505 тоже кратна этому числу. Это очевидно из формулы для магической константы нормального (традиционного) магического квадрата:

 

S = n*(n²+1)/2

 

Предлагаю читателям выполнить следующее окаймление, то есть построить магический квадрат 12-ого порядка. Понятно, что теперь надо пользоваться правилами для порядков серии n=4k. В качестве исходного магического квадрата 10-ого порядка возьмите только что построенный квадрат с рис. 45. На рис. 46 дана заготовка для построения магического квадрата 12-ого порядка. Осталось заполнить свободные ячейки.

 

 

                                                   Рис. 46

 

Здесь магические константы вписанных нетрадиционных магических квадратов такие: S₄ = 290, S₆ = 435, S₈ = 580, S₁₀ = 725. Все константы кратны числу n² + 1 = 145, причём множители кратности таковы: 2, 3, 4, 5. Наконец, магическая константа квадрата 12-ого порядка тоже кратна этому числу с множителем кратности 6: S₁₂ = 6*145 = 870.

 

Те, кому понравилось строить окаймлённые квадраты, могут пойти дальше: построить магические квадраты 14-ого порядка, 16-ого порядка и т. д.

 

МЕТОД СОСТАВНЫХ КВАДРАТОВ

 

Универсальный метод составных квадратов, конечно, работает и для квадратов чётно-чётного порядка. Минимальный порядок квадрата чётно-чётного порядка, который можно построить методом составных квадратов, равен 12.

Приведу пример построения магического квадрата методом составных квадратов. Поскольку число 12 представляется в виде произведения чисел 3 и 4, в качестве базового можно взять квадрат третьего порядка, а в качестве основного – квадрат четвёртого порядка. Можно и наоборот: в качестве базового взять квадрат четвёртого порядка, а в качестве основного – квадрат третьего порядка. Возьмём в качестве базового квадрат третьего порядка, который изображён на рис. 47.

 

 

                                                     Рис. 47

 

В качестве основного возьмём квадрат четвёртого порядка с рис. 36. На рис. 48 вы видите составной квадрат 12-ого порядка.

 

 

                                                                       Рис. 48

 

В этом примере базовый квадрат ассоциативный, основной квадрат – пандиагональный. Составной квадрат не обладает ни ассоциативностью, ни пандиагональностью. Чтобы некоторое свойство было присуще составному квадрату, этим свойством должны обладать и базовый, и основной квадраты.

 

Предлагаю читателям поменять ролями базовый  и основной квадраты и построить новый составной квадрат 12-ого порядка.

 

ПОСТРОЕНИЕ С ПОМОЩЬЮ КОМПЬЮТЕРА

 

Когда я только начинала изучение магических квадратов, меня очень удивил тот факт, что магических квадратов четвёртого порядка 880. В то время я работала программистом на старенькой ЭВМ. Составила программу для построения всех магических квадратов четвёртого порядка прямо в лоб, безо всяких методов. Старенькая ЭВМ выполняла программу очень долго, но всё-таки построила все 880 квадратов! В рукописи моей книги “Компьютер решает головоломки” есть эта программа и все 880 квадратов четвёртого порядка.

 

Впервые все 880 магических квадратов четвёртого порядка построил Френикль. Интересно узнать, как он их строил. Ведь ЭВМ тогда ещё не было.

Вот ссылка на статью Е. Я. Гуревича “Тайна древнего талисмана”, посвящённую исследованиям Френикля квадратов четвёртого порядка

 

http://www.telesmi.narod.ru/mystic/tlsmn010.htm

 

Среди 880 магических квадратов четвёртого порядка есть 48 ассоциативных и 48 пандиагональных (они же являются и совершенными). Вы можете найти эти квадраты в Приложении к моей книге “Волшебный мир магических квадратов”.

 

С помощью ЭВМ американские математики построили также все магические квадраты 5-ого порядка. Их оказалось несколько миллионов. Среди такого огромного количества магических квадратов 5-ого порядка есть только 3600 пандиагональных (с учётом параллельных переносов на торе) и всего 16 идеальных.

 

О своей программе построения магических квадратов 6-ого порядка расскажу в следующем разделе, посвящённом квадратам чётно-нечётного порядка.

 

Многие алгоритмы построения, разработанные разными исследователями магических квадратов, тоже реализуются с помощью компьютерных программ. Например, один читатель реализовал мой алгоритм построения идеальных квадратов порядка n=8k, k=1, 2, 3… и построил по составленной программе идеальный магический квадрат 6400-ого порядка. Выполнить такие построения без компьютера невозможно.

 

***

 

В заключение напомню читателям, что здесь не освещены методы построения пандиагональных, идеальных и совершенных магических квадратов чётно-чётного порядка. Об этих методах написаны специальные статьи. Зайдите в книгу “Волшебный мир магических квадратов” (http://www.klassikpoez.narod.ru/glavnaja.htm ) и там найдёте соответствующие статьи.

 

Продолжение будет здесь:

 

http://www.natalimak1.narod.ru/metody6.htm

 

***

 

Уважаемые читатели! Может быть, кто-нибудь поможет скачать книгу Н. М. Рудина “От магического квадрата к шахматам”, М.: Просвещение, 1969.

 

 

 

Я нашла эту книгу здесь: http://mirknig.com/

Но скачать книгу не удалось, ссылка оказалась битой. Книга помещена на этой сайт давно – 19 февраля 2006 г. Может быть, я что-то не так делаю. Подскажите, пожалуйста, как скачать книгу. Желательно дать прямую ссылку.

 

Ваша Наталия Макарова

 

9 – 13 сентября 2008 г.

г. Саратов

 

ДОБАВЛЕНИЕ (22 сентября 2008 г.)

 

МЕТОД СОТОВЫХ КВАДРАТОВ

 

Рассмотрев в следующем разделе очень интересный метод сотовых квадратов (называемый автором книги Чебраковым модифицированным методом террас) для построения магических квадратов чётно-нечётного порядка, я прочла в этой книге, что данный метод работает и для квадратов чётно-чётного порядка. Поэтому решила добавить метод сотовых квадратов в настоящий раздел. Прежде чем продолжать чтение, необходимо познакомиться с описанием метода в следующем разделе, так как здесь не повторяется подробное изложение метода. Смотрите страницу:

http://www.natalimak1.narod.ru/metody6.htm

 

Автор книги рассматривает для квадратов чётно-чётного порядка отдельно два случая: a) построение магических сотовых квадратов порядка n = 8k, k=1, 2, 3… б) построение магических сотовых квадратов порядка n = 8k + 4, k=1, 2, 3… Магический квадрат четвёртого порядка данным методом не строится. Рассмотрим первый случай.

 

Первый квадрат в серии порядков n = 8k, k=1, 2, 3… - квадрат 8-ого порядка. Для построения магического квадрата 8-ого порядка надо взять в качестве исходного любой магический квадрат 4-ого порядка. В книге пример построения квадрата данной серии порядков не приводится, поэтому будем строить его сами. Возьмём в качестве исходного квадрат 4-ого порядка квадрат, изображённый на рис. 49.

 

 

                                                     Рис. 49

 

Теперь надо заменить в этом квадрате числа от 1 до 16 на числа 1, 5, 9, 13, …, то есть на числа, являющиеся членами арифметической прогрессии с разностью d = 4. Замену надо производить в порядке следования тех и других чисел; ниже вы видите обе последовательности чисел, записанные по порядку; каждое число верхнего ряда заменяется на стоящее под ним число нижнего ряда.

 

    1      2          3          4          5          6          7          8          9          10        11        12        13        14        15        16

    1      5          9          13        17        21        25        29        33        37        41        45        49        53        57        61

 

На рис. 50 изображён получившийся в результате замены чисел квадрат. Это нетрадиционный магический квадрат с магической константой 124.

 

 

                                                     Рис. 50

 

Из этого квадрата строится первый вспомогательный сотовый квадрат следующим образом: каждая ячейка квадрата превращается в квадрат 2х2 и в каждой ячейке этого квадрата записывается число из исходной ячейки. Готовый первый вспомогательный сотовый квадрат смотрите на рис. 51.

 

 

                                                     Рис. 51

 

Этот квадрат является нетрадиционным магическим квадратом с магической константой 248.

 

Приступаем к построению второго вспомогательного сотового квадрата. Этот квадрат составляется тоже из квадратов 2х2, но во всех этих квадратах записываются всего четыре числа: 0, 1, 2, 3. В книге приведена схема расстановки блоков 2х2 в квадрате 8-ого порядка так, чтобы этот квадрат был магическим. Вот эта схема (рис. 52):

 

 

                                                     Рис. 52

 

Здесь записаны номера блоков 2х2 (см. рис. 29 в указанной выше статье). Заменив номера блоков самими блоками, получаем второй вспомогательный сотовый квадрат (рис. 53).

 

 

                                                     Рис. 53

 

Мы имеем нетрадиционный магический квадрат с магической константой 12.

Теперь осталось сложить поэлементно два вспомогательных квадрата (рис. 51 и рис. 53). На рис. 54 вы видите готовый магический квадрат 8-ого порядка. Его тоже можно назвать сотовым, так как он состоит из блоков 2х2, в каждом из которых записаны четыре последовательных числа.

 

 

                                                     Рис. 54

 

Второй пример тоже для квадрата 8-ого порядка, но в качестве исходного квадрата 4-ого порядка возьмём квадрат, построенный методом квадратных рамок (рис. 55).

 

 

                                                     Рис. 55

 

Этот магический квадрат ассоциативный. Произведём замену чисел (интересно отметить, что в данном случае можно вместо замены чисел построить нетрадиционный магический квадрат методом квадратных рамок применительно к числам 1, 5, 9, … , 61). Квадрат, получившийся в результате замены чисел показан на рис. 56.

 

 

                                                     Рис. 56

 

Превращаем этот квадрат в первый вспомогательный сотовый квадрат (рис. 57):

 

 

                                                     Рис. 57

 

Обратите внимание: этот нетрадиционный магический квадрат так же ассоциативный.

Сложим два вспомогательных квадрата (рис. 53 и рис. 57). Готовый магический квадрат 8-ого порядка вы видите на рис. 58.

 

 

                                                     Рис. 58

 

Этот сотовый магический квадрат тоже ассоциативный.

 

Возникает вопрос: если взять в качестве исходного квадрата 4-ого порядка пандиагональный квадрат, получится ли магический квадрат 8-ого порядка, построенный методом сотовых квадратов, пандиагональным? Для этого необходимо, чтобы второй вспомогательный сотовый квадрат (см. рис. 53) тоже был пандиагональный. Можно ли построить такой второй вспомогательный сотовый квадрат? Интересный вопрос! Предлагаю читателям заняться этой задачей.

 

Приведу ещё один пример: построение методом сотовых квадратов магического квадрата следующего порядка в рассматриваемой серии порядков – 16-ого. В качестве исходного возьмём квадрат 8-ого порядка, построенный методом квадратных рамок (см. рис. 2). Вместо замены чисел в этом квадрате поступим так: построим нетрадиционный магический квадрат 8-ого порядка методом квадратных рамок применительно к числам 1, 5, 9, 13, … (рис. 59). Мне кажется, что строить квадрат методом квадратных рамок намного удобнее, чем производить замену чисел в магическом квадрате с рис. 2.

 

 

Рис. 59

 

Примечание: как строятся квадратные рамки, смотрите на рис. 1.

 

Превращаем построенный нетрадиционный магический квадрат в первый вспомогательный сотовый квадрат (рис. 60).

 

 

                                                     Рис. 60

 

Перед вами нетрадиционный ассоциативный магический квадрат с магической константой 2032.

 

Второй вспомогательный сотовый квадрат 16-ого порядка в [1] рекомендуется строить из четырёх сотовых квадратов 8х8 (рис. 61).

 

 

Рис. 61

 

Очевидно, что этот нетрадиционный магический квадрат тоже ассоциативный.

Сложим поэлементно два вспомогательных квадрата (рис. 60 и рис. 61) и магический сотовый квадрат 16-ого порядка готов (рис. 62).

 

 

Рис. 62

 

Полученный сотовый магический квадрат тоже ассоциативный.

 

Вернёмся к задаче построения пандиагонального сотового квадрата 8-ого порядка. Как уже сказано, для этого необходимо, чтобы исходный магический квадрат 4-ого порядка был пандиагональным и второй вспомогательный сотовый квадрат тоже был пандиагональным. Начнём с построения первого вспомогательного квадрата. В качестве исходного квадрата 4-ого порядка возьмём следующий пандиагональный квадрат (рис. 63):

 

 

                                                     Рис. 63

 

Процесс построения первого вспомогательного квадрата не буду описывать подробно, так как это уже было описано выше. Готовый первый вспомогательный квадрат изображён на рис. 64.

 

 

                                                     Рис. 64

 

Этот нетрадиционный магический квадрат ещё и пандиагональный, его магическая константа равна 248.

 

Теперь надо построить второй вспомогательный сотовый квадрат так, чтобы он тоже был пандиагональный. Для этого применим к ассоциативному сотовому квадрату с рис. 53 преобразование трёх квадратов (это преобразование было разработано мной при исследовании ассоциативных и пандиагональных квадратов чётно-чётного порядка; оно превращает ассоциативный квадрат чётно-чётного порядка в пандиагональный). В результате применения этого преобразования получаем пандиагональный сотовый квадрат (рис. 65).

 

 

                                                     Рис. 65

 

Примечание: интересно показать, какая будет схема расстановки “кирпичиков” в этом сотовом квадрате (рис. 65а):

 

 

                                                     Рис. 65а

 

Сравните эту схему со схемой из [1] на рис. 52. Здесь, в отличие от схемы из книги, используются четыре разных “кирпичика”: №№ 6, 13, 14, 20.

 

Сложив эти два вспомогательных квадрата, получим пандиагональный сотовый квадрат 8-ого порядка (рис. 66).

 

 

                                                     Рис. 66

 

Удивительный пандиагональный квадрат с оригинальной начальной цепочкой. На следующем рисунке (рис. 66а) изображён этот квадрат с выделенной начальной цепочкой. Начальная цепочка тоже напоминает ход коня, но ход этот делается целыми блоками 2х2. Примечательно, что в исходном пандиагональном квадрате 4-ого порядка (см. рис. 63) начальная цепочка строится точно таким ходом коня.

 

 

                                                     Рис. 66а

 

Пандиагональный сотовый квадрат мне ещё нигде не встречался.

 

Интересно отметить, что другой сотовый пандиагональный квадрат 8-ого порядка можно получить из ассоциативного сотового квадрата с рис. 58, применив к нему преобразование трёх квадратов. Смотрите этот новый пандиагональный сотовый квадрат на рис. 66б.

 

 

                                                     Рис. 66б

 

Продублирую этот пандиагональный квадрат с выделенной начальной цепочкой (рис. 66в).

 

 

                                                     Рис. 66в

 

Начальная цепочка в этом квадрате изменила свою форму, тоже ход конём, но по-другому.

 

Аналогично построим пандиагональный сотовый квадрат 16-ого порядка. Сначала строим первый вспомогательный квадрат. В качестве исходного возьмём следующий пандиагональный квадрат 8-ого порядка (рис. 67):

 

 

                                                     Рис. 67

 

На рис. 68 вы видите первый вспомогательный сотовый квадрат. Он является нетрадиционным пандиагональным магическим квадратом с магической константой 2032.

 

 

Рис. 68

 

Второй вспомогательный сотовый квадрат построим из квадрата с рис. 61, применив преобразование трёх квадратов. Готовый нетрадиционный пандиагональный магический квадрат – второй вспомогательный – вы видите на рис. 69. Его магическая константа равна 24.

 

 

Рис. 69

 

Примечание: посмотрим на схему расстановки “кирпичиков” в этом сотовом квадрате (рис. 69а):

 

 

Рис. 69а

 

Очевидно, что эта схема отлична от схемы из книги. Гармонично составлена эта схема, при её составлении использованы четыре разных “кирпичика”: №№ 6, 13, 14, 20.

 

Сложим два вспомогательных квадрата, и пандиагональный магический квадрат 16-ого порядка готов (рис. 70).

 

 

Рис. 70

 

Продублирую этот квадрат с выделенной начальной цепочкой (рис. 71).

 

 

Рис. 71

 

Сравните начальную цепочку в этом квадрате с начальной цепочкой в исходном пандиагональном квадрате 8-ого порядка (рис. 67). Здесь такой же ход коня, только ход этот делается целыми блоками 2х2.

 

И точно так же, как для квадратов 8-ого порядка, построим второй пандиагональный сотовый квадрат 16-ого порядка из ассоциативного сотового квадрата с рис. 62, применив к нему преобразование трёх квадратов. Новый сотовый пандиагональный квадрат изображён на рис. 72.

 

 

Рис. 72

 

В этом сотовом пандиагональном квадрате выделена оранжевым цветом начальная цепочка. Она имеет совсем другую форму, нежели предыдущий сотовый пандиагональный квадрат (рис. 71).

 

Теперь такой вопрос: можно ли построить идеальный сотовый квадрат? Понятно, что для этого надо, чтобы оба вспомогательных сотовых квадрата были нетрадиционными идеальными магическими квадратами. Поскольку идеального квадрата 4-ого порядка не существует, то идеальный сотовый квадрат 8-ого порядка построить нельзя (по крайней мере, данным методом). Тогда посмотрим, что у нас получится для сотового квадрата 16-ого порядка. Построить идеальный первый вспомогательный квадрат нетрудно. Возьмём в качестве исходного идеальный квадрат 8-ого порядка, изображённый на рис. 73.

 

 

Рис. 73

 

Превращаем этот идеальный квадрат в первый вспомогательный сотовый квадрат 16-ого порядка (рис. 74).

 

 

Рис. 74

 

Нетрадиционный идеальный сотовый магический квадрат получился, его магическая константа равна 2032. Теперь задача в том, чтобы построить второй вспомогательный сотовый квадрат 16-ого порядка так, чтобы он тоже был идеальным нетрадиционным магическим квадратом с магической константой 24. Мы уже имеем ассоциативный второй вспомогательный квадрат (рис. 61) и пандиагональный второй вспомогательный квадрат (рис. 69), а вот идеального пока не имеем. Оставляю эту задачу читателям.

 

ЗАДАЧА

 

 

Если вам удастся составить такой квадрат, то, сложив этот квадрат с первым вспомогательным квадратом с рис. 74, вы получите идеальный сотовый магический квадрат 16-ого порядка. Совершенно новый тип идеального квадрата!

 

Как-нибудь на досуге я тоже попробую решить эту задачу.

 

Мне осталось изложить метод сотовых квадратов для порядков n = 8k + 4, k=1, 2, 3… Сделаю это на следующей странице:

 

http://www.natalimak1.narod.ru/met5a.htm

 

***

 

       Пишите мне!

Приглашаю всех на форум!

На главную страницу