КОЛЛЕКЦИЯ МАГИЧЕСКИХ КВАДРАТОВ
приложение к книге “Волшебный мир магических квадратов”
Хочу создать коллекцию магических квадратов, построенных мной. Правда, я почти совсем не умею создавать картинки в Фотошопе и поэтому очень надеюсь на вашу помощь, дорогие мои читатели. Многие из вас, наверное, с Фотошопом на “ты” и могут создавать прекрасные картинки. Так ведь?
Сначала покажу две замечательные картинки, которые сделал мой читатель Виктор Ивченко. Он изобразил на призме идеальный квадрат пятого порядка. Вот эти картинки (два вида):


Здорово! Я такие картинки создавать не умею. Эти картинки созданы не в Фотошопе, а в пакете программ Mathcad. У меня даже и пакета такого нет.
А теперь покажу свои первые опыты.
№ 1 - сотовый пандиагональный квадрат 8-ого порядка (рис. 1):
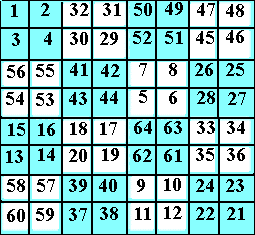
Рис. 1
№ 2 – идеальный квадрат 7-ого порядка (рис. 2):

Рис. 2
№ 3 – идеальный квадрат 8-ого порядка (рис. 3):

Рис. 3
Примечание: этот квадрат построен по алгоритму Франклина. Смотрите статью http://www.klassikpoez.narod.ru/idealch1.htm
Да, совсем забыла, что самая первая картинка с магическим квадратом была создана мной, когда я делала добавления в статью “Магический квадрат” в Википедии. Вот эта картинка (рис. 4):

Рис. 4
На этом рисунке показано, как образуются разломанные диагонали пандиагонального магического квадрата четвёртого порядка. Очень плохая картинка, но это мой самый первый опыт работы в Фотошопе. Картинка, однако, в Википедии прижилась.
Далее попробую показать идеальные квадраты 9-ого порядка. Таких квадратов я построила очень много. Конечно, показывать буду только оригинальные квадраты. На рис. 5 вы видите самый первый идеальный квадрат 9-ого порядка, который мне удалось построить с помощью матричного метода найденного в Интернете. Я буду вести сквозную нумерацию квадратов коллекции.
Квадрат № 4

Рис. 5
В квадрате выделена зелёным цветом начальная цепочка. Напомню читателям, что начальной цепочкой магического квадрата порядка n называется последовательность первых n чисел. Начальная цепочка может быть самой причудливой формы. Есть диагональные и линейные начальные цепочки, есть начальная цепочка, образуемая ходом шахматного коня. И ещё много разных форм может принимать начальная цепочка в магическом квадрате. В квадрате № 2 начальная цепочка образуется ходом шахматного коня, в квадрате № 3 начальная цепочка имеет линейную форму, в квадрате № 1 – тоже ход конём, но ход этот делается целым блоком 2х2.
Следующие идеальные квадраты из статьи “Ещё раз об идеальных квадратах 9-ого порядка”:
http://www.natalimak1.narod.ru/id9new.htm
Квадрат № 5

Рис. 6
Посмотрите, насколько причудлива начальная цепочка в этом квадрате!
А следующий квадрат получен из квадрата № 5 комбинацией преобразований, он превратился в результате этих преобразований в идеальный квадрат, начинающийся с числа 1, то есть число 1 стоит в левой верхней ячейке квадрата. Магические квадраты, начинающиеся с числа 1, – мои самые любимые квадраты. Везде, где можно, я стараюсь приводить квадраты к такому виду.
Квадрат № 6

Рис. 7
И опять новая форма начальной цепочки.
Следующий квадрат построен с использованием двух ортогональных латинских квадратов. Построена по программе группа из 48 подобных квадратов, все квадраты этой группы можно посмотреть здесь:
http://www.natalimak1.narod.ru/mk/id9pril.htm
Квадрат № 7

Рис. 8
В этом квадрате начальная цепочка строится ходом шахматного коня. Квадрат может быть построен также методом стандартных качелей. В моих исследованиях установлена определённая связь между методом качелей и методом латинских квадратов.
И опять превращаю этот идеальный квадрат в другой идеальный квадрат, начинающийся с числа 1, комбинацией преобразований. Новый квадрат вы видите на рис. 9. Получился совершенно новый тип идеального квадрата с линейной начальной цепочкой. С точки зрения метода качелей изменились шаги качания качелей. Понятно, что этот квадрат тоже можно построить методом качелей (только уже нестандартных, стандартные качели относятся к квадратам с начальной цепочкой “ход конём”).
Квадрат № 8

Рис. 9
Продолжение следует
Жду ваших картинок, уважаемые читатели! Магические квадраты для картинок берите в моей книге “Волшебный мир магических квадратов”: http://www.klassikpoez.narod.ru/glavnaja.htm
Это должны быть оригинальные магические квадраты, построенные мной.
ДОБАВЛЕНИЕ (10 мая 2009 г.)
Ох, совсем забросила я свою коллекцию! В последнее время занялась исследованиями латинских квадратов. Всё началось с углубленного изучения метода латинских квадратов. Написан цикл статей “Новые аспекты метода латинских квадратов”. А потом втянулась в исследование латинских квадратов всё больше и уже не могу прерваться. А для создания картинок у меня появилась прекрасная программа-фотоаппарат, один виртуальный друг подарил. Теперь так просто создавать картинки, щёлк фотоаппаратом – и готово! Недавно показала одну такую картинку в ЖЖ. Подумала, что надо внести эту картинку в коллекцию. Это идеальный квадрат 16-го порядка, построенный из пандиагонального квадрата Франклина. Выше показан такой квадрат 8-го порядка (квадрат № 3). Поскольку квадрат построен из квадрата Франклина, я назвала его квадратом Франклина.
Квадрат № 9

Это самый прекрасный магический квадрат из всех, созданных человечеством. Сам Франклин был очарован своим пандиагональным магическим квадратом 16-го порядка. Однако его квадрат не был идеальным. Может быть, во времена Франклина ещё не были известны идеальные магические квадраты. Чтобы превратить пандиагональный квадрат Франклина в идеальный магический квадрат, надо выполнить совсем несложные преобразования. Напомню ещё раз, что, получив идеальный квадрат 16-го порядка, я разработала на основе этого единственного примера алгоритм построения идеальных магических квадратов любого порядка n = 8k, k = 1, 2, 3, …
Может быть, ещё вернусь к этой коллекции и продолжу её. А пока опять принимаюсь за латинские квадраты. Совсем недавно обнаружила, что есть совершенные латинские квадраты. Вот надо написать о них статью. Я не прощаюсь. Ждите продолжения!
Ваша Наталия Макарова
13 - 14 октября 2008 г. – 10 мая 2009 г.
г. Саратов
Читайте мою виртуальную книгу “Волшебный мир магических квадратов”:
http://www.klassikpoez.narod.ru/glavnaja.htm
Скачайте электронную версию этой книги:
http://narod.ru/disk/5834353000/Magic_squares.pdf.html
Заодно прихватите книгу “Позиционные системы счисления”, авось, пригодится:
http://narod.ru/disk/5936760000/pozic4.pdf.html
Пишите мне!
На главную страницу